ベクトルの大きさとは
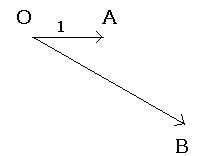

|
|
ベクトルの成分
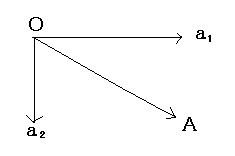
|
|
ベクトルの大きさ

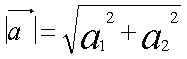
|
|
原点から出発しないベクトルの成分
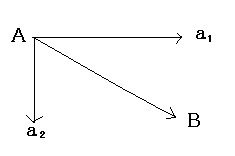
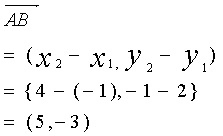
|
|
原点から出発しないベクトルの大きさ
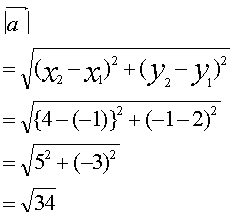
|
|
ベクトルの大きさとは


|
|
ベクトルの成分

|
|
ベクトルの大きさ

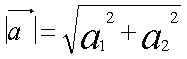
|
|
原点から出発しないベクトルの成分

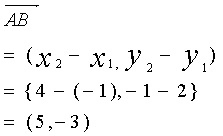
|
|
原点から出発しないベクトルの大きさ

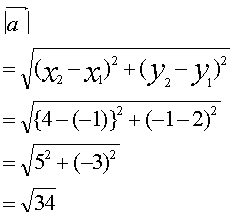
|
|
成分は(a1,a2)、大きさは線分の長さになります。